복잡도(Complexity)

(아직도 작성 중)

1. 복잡도

처리해야 할 데이터의 양이 방대해지면서, 알고리즘의 효율성 차이가 커질 수 밖에 없습니다. 가령, 데이터를 정렬하더라도 정렬 알고리즘마다 정렬에 걸리는 시간은 천차만별입니다. 방대한 데이터를 더 빨리 처리할 수 있는 방법을 선택해야겠습니다.

서로 다른 알고리즘을 비교할 때, 하드웨어와 소프트웨어 환경이 천차만별이라면 결과를 신뢰하기 힘들겁니다. 계산복잡도는 이러한 환경을 배제하고 알고리즘이 얼마나 효율적인지 알 수 있습니다.

계산복잡도의 기준은 알고리즘이 소모하는 소요시간과 메모리 사용량 등 자원으로 구분합니다. 전자를 시간복잡도(Time complexity), 후자를 공간복잡도(Space complexity)라고 합니다.

1. 1. 점근 표기법 - 빅오 표기법(Big-O notation)

점근표기법은 오메가 표기법, 세타 표기법, 빅오 표기법이 있습니다. 각각 최선, 평균, 최악의 경우 복잡도를 나타냅니다. 어떤 환경에서 사용할 알고리즘인지에 따라 다르겠지만, 보통 빅오 표기법으로 복잡도를 판단합니다.

빅오 표기법은 시공간 복잡도를 수학적으로 표기하는 대표적인 방법입니다. 알고리즘의 성능을 논리적으로 예측하기 위해 사용합니다. 빅오 표기법에는 다음과 같은 두 가지 규칙이 있습니다.

1. 영향력이 가장 큰 최고차항 이외의 항들은 무시합니다.
   • $f(n)=n^2 + n$ —-> $O(n^2)$
2. 최고차항의 계수와 상수항은 무시합니다.
   • $f(n)=3n + 10$ —-> $O(n)$

$3n +10$의 복잡도를 가진다고 하지 않는 이유는 정확한 단계 수를 결정하기가 어렵기 때문입니다. 정확한 단계를 알고자 들여야하는 비용이 낭비를 초래할 수 있습니다. 그보다는 ‘이 알고리즘은 $n$에 비례한다.’라는 정보만으로 충분히 성능을 가늠할 수 있습니다.

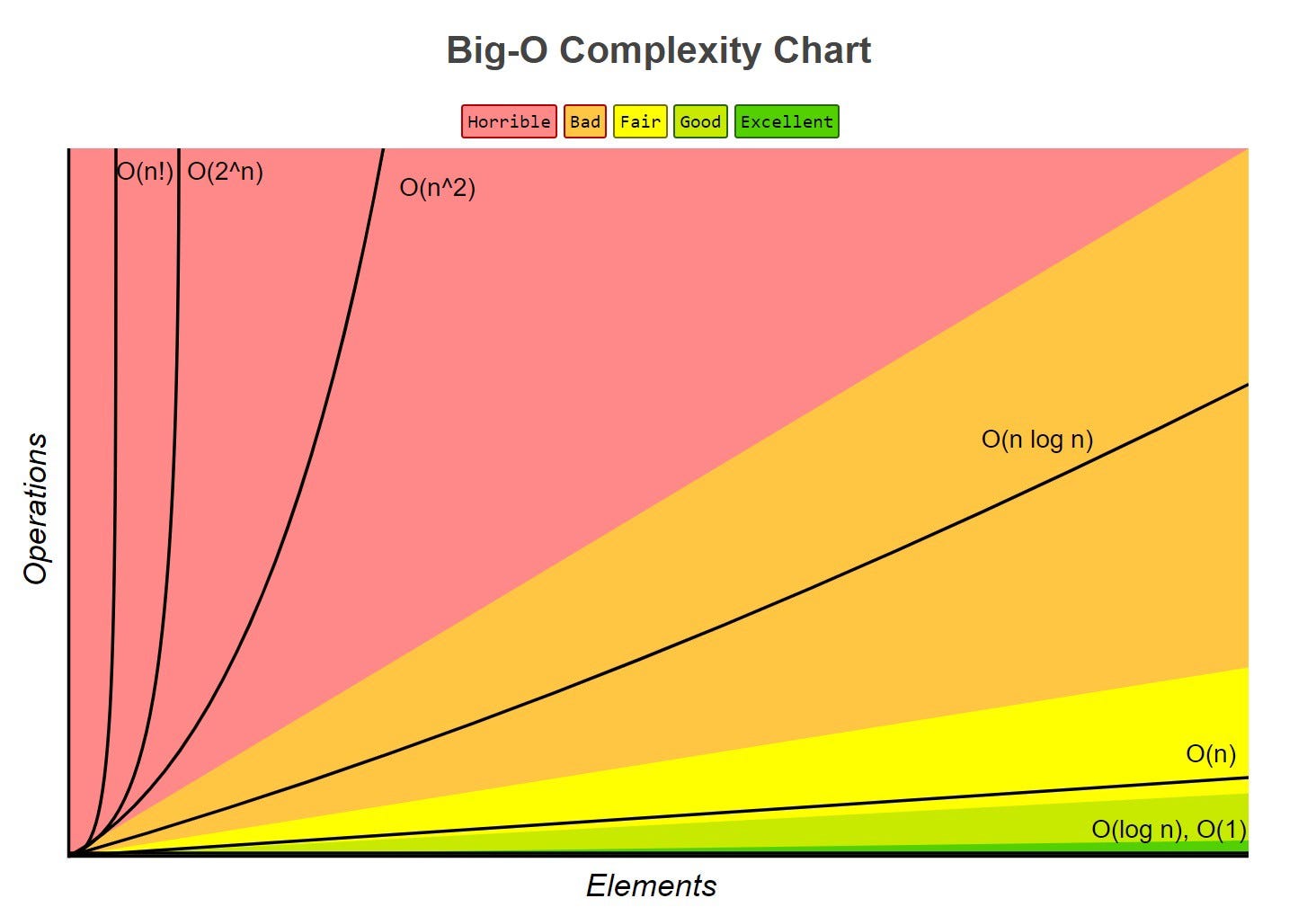한편, 대부분의 알고리즘은 아래와 같은 수식으로 나타낼 수 있습니다. 위로 갈 수록 간단하고, 아래로 갈 수록 복잡해집니다. ($log_2n$은 $logn$을 의미합니다.)

$O(1)$과 같은 상수 형태 (정수가 짝수이거나 홀수인지 판단)
$O(logn)$과 같은 로그 형태 (이진탐색 - 자료의 수가 $2^n$이면, 복잡도는 $log_2(2^n) = n$)
$O(n)$과 같은 선형 형태 (정렬되지 않은 배열에서 최솟값이나 최댓값 탐색)
$O(nlogn)$과 같은 선형로그 형태 (퀵 정렬, 병합정렬, 힙 정렬 등)
$O(n^c)$과 같은 다차 형태 (이중반복문이나 버블 정렬, 선택 정렬, 삽입 정렬 등)
$O(c^n)$과 같은 지수 형태
$O(n!)$과 같은 팩토리얼 형태

1. 2. 공간복잡도(Space complexity)

공간복잡도는 어떤 프로그램을 실행시킨 후 완료하기까지 필요로 하는 자원공간의 양입니다. 메모리 공간을 얼마나 효율적으로 사용하는지 나타내는 개념인 것이죠. 총요구공간 $S(P)$은 고정요구공간 $c$와 가변요구공간 $S_p(n)$의 합으로 나타낼 수 있습니다.

$S(P) = c + S_p(n)$

고정공간은 입출력의 횟수와 크기에 관계없는 요구공간을 말합니다. 코드 저장공간, 단순변수, 고정크기의 구조변수, 상수가 해당된다고 합니다. 가변공간은 해결하려는 문제의 특정 인스턴스에 따라 가변적인 크기를 가진 구조화 변수들을 필요로 하는 공간, 함수가 순환호출을 할 경우 요구되는 추가공간을 말합니다.

$n!$을 계산하는 함수를 반복문과 재귀함수로 작성하여 비교해봅시다.

// 재귀함수
function factorialByRecursion(n) {
  if ( n === 1 ) {
    return 1;
  };
  return factorial(n - 1);
};

//반복문으로 작성한 함수
function factorialByLoop(n) {
  let result = 1;
  for ( let i = 0; i <= n; i++ ) {
    result = result * i;
  };
  return result;
};

재귀함수로 작성한 함수는 n === 1이 될 때 까지 서브함수를 호출합니다. 따라서 스택에는 실행 컨텍스트가 n에서 1까지 쌓이게 됩니다. 공간복잡도는 $O(n)$이 됩니다. 반복문으로 구현한 함수는 n의 값에 상관없이 실행 컨텍스트는 하나만 존재합니다. 공간복잡도가 $O(1)$인 것이죠.

1. 3. 시간복잡도(Time complexity)

시간복잡도는 알고리즘을 수행하는 데 얼마나 많은 연산이 수행되어야 하는지 숫자로 표기합니다. 하드웨어, 프로그래밍 언어 등 환경에 따라 편차가 크기 때문에 명령어의 실행 횟수만으로 판단합니다.

유사한 기능을 수행하는 알고리즘 간의 성능차이를 확연히 느끼고 싶다면, 정렬 알고리즘을 확인해봅시다.

2. 더 알아보기 - 정렬 알고리즘(Sorting algorithm)

처음으로 정렬 알고리즘을 구현할 때 중첩반복문으로 구현했습니다. n개의 자료를 정렬한다면 시간반복도는 $O(n^2)$이 되겠죠. 테스트 케이스 규모가 작아서 느끼지 못했지만, 수십, 수백만 개 자료를 정렬한다면 굉장히 비효율적일겁니다.

다음 예제들을 보면서 어떤 정렬 알고리즘이 있고, 어떻게 작동되는지 알아봅시다.

2. 1. 시간반복도 $O(n^2)$ 정렬

2. 1. 1. 버블 정렬(Bubble Sort)

1번째와 2번째 원소를 비교하여 정렬하고, 2번째와 3번째, …, n-1번째와 n번째를 확인하여 정렬한 뒤 다시 처음으로 돌아가 n-2번째와 n-1번째까지, …를 반복하는 정렬입니다. 매 순회마다 마지막 하나가 정렬되어 원소들이 거품처럼 올라오는 것처럼 보입니다.

function bubbleSort(arr) {
  let length = arr.length - 1;
  let temp;
  for ( let i = 0; i < length; i++ ) {
    for ( let j = 0; j < length - 1 - i; j++ ) {
      if (arr[j] > arr[j + 1]) {
        temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      };
    };
  };
  return arr;
};

2. 1. 2. 칵테일 정렬(Cocktail shaker sort)

홀수 번째 요소는 앞에서부터 확인하고, 짝수 번째 요소는 뒤에서부터 확인합니다. 버블 정렬이 마지막에서 처음으로 정렬했다면, 칵테일 정렬은 처음과 마지막을 번갈아가면서 정렬합니다.

function shakerSort(arr) {
  const length = arr.length - 1;
  let isSorted = false;
  
  while (!isSorted) {
    isSorted = true;
    for ( let i = 0; i < length; i++ ) {
      if (arr[i] > arr[i + 1]) {
        let temp = arr[i];
        arr[i] = arr[i + 1];
        arr[i + 1] = temp;
        isSorted = false;
      };
    };
    
    if (isSorted) {
      break;
    };
    isSorted = true;

    for ( let j = length - 1; j >0; j-- ) {
      if ( arr[j - 1] > arr[j] ) {
        let temp = arr[j];
        arr[j] = arr[j-1];
        arr[j-1] = temp;
        isSorted = false;
      };
    };
  };
  return arr;
};

2. 1. 3. 선택 정렬(Selection sort)

버블정렬이 매번 두 요소를 비교하여 위치를 바꾼다면, 선택 정렬은 처음부터 마지막까지 한 번 훑어 정렬하고, 그 다음은 2번째에서 마지막까지 순환하는 방식으로 정렬합니다. 정렬이 일관성있게 $n(n-1)/2$에 비례하는 시간이 걸립니다.

function selectionSort(arr) {
  for ( let i = 0; i < arr.length - 1; i++ ) {
    let minimumNumIdx = i;
    for ( let j = i + 1; j < arr.length; j++ ) {
      if ( arr[minimumNumIdx] > arr[j] ) {
        minimumNumIdx = j;
      };
    };
    if ( minimumNumIdx !== i ) {
      let temp = arr[minimumNumIdx];
      arr[minimumNumIdx] = arr[i];
      arr[i] = temp;
    };
  };
  return arr;
}; 

2. 1. 4. 삽입 정렬(Insertion sort)

$n$번째 원소를 첫 번째에서 $n-1$번째까지 비교하여 적절한 위치에 놓고, 그 뒤의 자료들을 한 칸씩 밀어내는 정렬방식입니다. $O(n^2)$ 중 빠른 편이지만, 오름차순 정렬일 때 작은 요소들이 뒤 쪽에 몰려있으면 많은 시간이 걸립니다.

다만, 자료구조가 이미 정렬되어있거나 규모가 작다면 굉장히 효과적인 알고리즘입니다. 고성능 알고리즘 중에서는 배열 규모가 클 때 $O(nlogn)$ 알고리즘을 사용하다가, 정렬해야 할 부분이 작으면 삽입정렬로 전환하기도 합니다.

function insertionSort(arr) {
  for ( let i = 1; i < arr.length; i++ ) {
    let currentEl = arr[i];
    let j = i-1;
    while ( (j > -1) && (currentEl < arr[j]) ) {
      arr[j + 1] = arr[j];
      j--;
    };
    arr[j + 1] = currentEl;
  };
  return arr;
};

2. 2. 시간반복도 $O(nlogn)$ 정렬

3. Reference

• https://velog.io/@raram2/big-o-notation-and-time-complexity
• https://madplay.github.io/post/time-complexity-space-complexity
• https://en.wikipedia.org/wiki/Time_complexity
• https://d2.naver.com/helloworld/0315536 - 정렬 알고리즘의 시간복잡도, 꼭 읽어봅시다.
• https://blog.chulgil.me/algorithm/
• https://stackabuse.com/bubble-sort-and-cocktail-shaker-sort-in-javascript/
• https://loving-wright-d0eedb.netlify.app/blog/selection-sort-in-javascript